Palindromic polynomial

A polynomial is palindromic, if the sequence of its coefficients are a palindrome.

Let 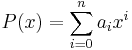P(x) = \sum_{i=0}^n a_ix^i be a polynomial of degree n, then P is palindromic if 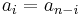a_i = a_{n-i} for i=0...n.

Similarly, P is called antipalindromic if 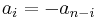a_i = -a_{n-i} for i=0...n.

Examples

Some examples of palindromic polynomials are:

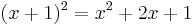
(x%2B1)^2 = x^2 %2B 2x %2B 1

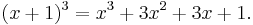
(x%2B1)^3 = x^3 %2B 3x^2 %2B 3x %2B 1.

Generally, the expansion of 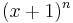(x%2B1)^n is palindromic for all n (can see this from binomial expansion)

It also follows that if P is of even degree (so has odd number of terms in the polynomial), then it can only be antipalindromic when the 'middle' term is 0, i.e. 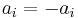a_i=-a_i, where n=2i.

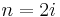See also

External links